Unbreakable cryptography: The devil and the details

Quantum cryptography has yet to deliver a truly unbreakable way of sending messages. Quantum entanglement may change that

RECENT revelations of online snooping on an epic scale, by government agencies which may well have been breaking the law, have prompted some users of the internet to ask who you can trust with sensitive data these days. According to Artur Ekert, an Oxford academic who moonlights as director of the Centre for Quantum Technologies (CQT) in Singapore, one possibility is a defunct Irish physicist called John Stewart Bell.

In 1964 Bell proposed a test to settle once and for all whether quantum mechanics really is as weird as it famously appears to be, in that it allows for instantaneous communication between two particles, no matter how far apart they are, on condition that they were once entangled together in the same place. The short answer, as experiments carried out over subsequent decades have shown, is yes, it is. Bell’s test, however, also led physicists like Dr Ekert to a remarkable insight: made sufficiently sensitive the Bell test could be used to guarantee perfectly secure communication—even if the equipment used to send and receive those communications had been sold to you by a manufacturer subverted by your enemies.

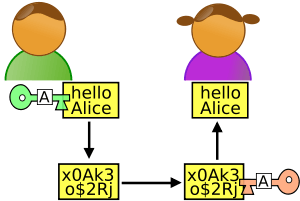
The current way quantum theory is employed in cryptography, known as “prepare and measure”, works by distributing a secret key, encoded in the way light is polarised, to two people (known conventionally as Alice and Bob) who wish to talk privily with each other. This key is used to encrypt a message so that it cannot be understood, even if it is intercepted. Prepare-and-measure looks good in theory because an eavesdropper (Eve) listening in will perforce give herself away by measuring the light’s polarisation, and thus disrupting the system. If that happens, Alice and Bob can ditch the compromised key and ask for another.

However, if Eve can somehow tinker with the sending and receiving equipment (for example by blinding it with a special kind of laser, as happened in one famous quantum hack in 2010, or getting the manufacturer to do something similar), she can hide her disruption, leaving Bob and Alice none the wiser. The technique therefore ceases to be secure. Given recent revelations about Western-government activities in this area, and strong suspicions about pressure the Chinese government puts on the country’s computer and telecoms firms, users’ fears that their equipment might not be all it says it is are hardly paranoid. The Bell test promises to assuage those fears.

For whom the Bell tallies

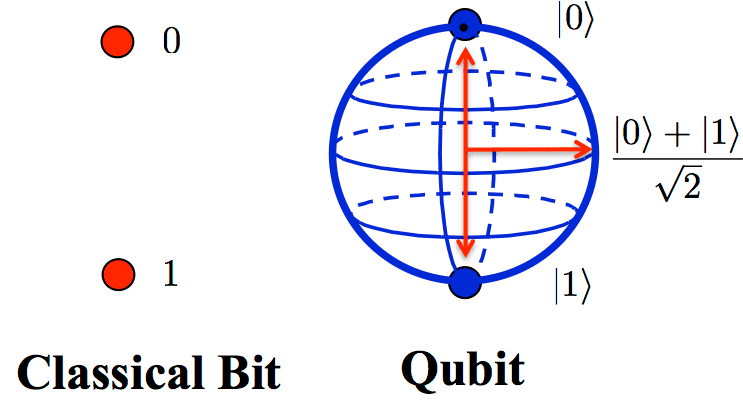
Bell-based cryptography also works by generating a key based on the polarisation of light. But it begins by using a special machine to produce the particles of light (called photons) in which the message will be encoded. This machine turns them out as entangled pairs. One member of each pair goes to Alice, and one to Bob. For each photon she receives, Alice chooses at random which of two predetermined polarisation angles to measure. For each measurement, she can get one of two results: either the photon will appear aligned with her polarisation axis (call that a one) or perpendicular to it (call it zero). This can be used to encode a digital bit. Bob, for his part, also measures his photon’s polarisation. Both of his axes, too, have been arbitrarily set.

Conventional odds in the world of classical physics predict Alice’s and Bob’s bits will match three times out of four. Add in quantum entanglement, though, and the odds increase to just over 85%. This was the essence of Bell’s insight.

If Alice and Bob’s measurements agree more often three-quarters of the time, it suggests their photons are entangled. That means they cannot have been intercepted, since any attempt by Eve to do so would inevitably cause them to untangle. If Alice and Bob then each add a third, identical polarisation angle, they can use this extra bit, which they know they must share, to encode the cryptographic key.

See Also

Real cybersecurity using only a single quantum bit gets real

Read more . . .